[샘토링 블로그] 항등식과 등식의 차이는 무엇인가요?
Q. 나눗셈 관계식에서 A=BQ+R ( B 나누는수, Q 몫 , R 나머지) 라는 식이 왜 항등식인가요?
그리고 항등식과 등식의 차이는 무엇인가요?
A. 네 좋은 질문입니다. 우리가 방정식 항등식 등식을 자유롭게 쓰지만 막상 설명하라 그러면 힘든 점이 많죠.
일단 사전적 의미를 봅시다.
항등식 방정식 등식의 사전적 의미 항등식 : 식 중의 문자에 어떤 값을 넣어도 언제나 성립하는 등식 방정식 : 미지수를 함유하는 등식(等式)에서, 그 미지수에 특정한 수치(數値)를 넣었을 때에만 성립하는 것 등식 : 식과 문자나 수가 등호로 이어진 것. |
항등식은 항상 성립하는 식을 뜻하고
방정식은 미지수에 특정수를 집어넣을 때만 성립하는 식입니다.
예를 들어 볼게요
① $2(x-2)=2x-4$
② $x-2=4$
①번식 같은 경우는 x에 어떤 수를 넣더라도 다 성립합니다.
즉 왼쪽 오른쪽 같은 식 인거죠.
이렇듯 어떤 수를 넣어도 성립하는 식을 항등식이라고 부릅니다.
반면 ②번식 같은 경우는 x 에 6을 넣어야지만 성립하죠?
이런 식은 방정식이라고 부릅니다.
항등식 방정식은 여러분들이 문제를 풀 때 너무나도 많이 사용하는 것 중 하나에요. 그렇지만 그냥 자연스럽게 쓰고 있었던 거죠.
식을 정리 할때는 항등식을 이용해 정리 했던거고, 마지막에 답을 낼 때는 방정식을 이용해 미지수를 찾았던 거죠.
그럼 항등식과 등식은 무엇이냐?
등식은 항등식과 비교되는 식은 아니구요,
등식은 부등식과 비교되는 식입니다.
등호(=)를 이용해 나타낸 식이 등식이구요
부등호( $\le$ )를 이용해 나타낸 식이 부등식입니다.
그러니 항등식이나 방정식 모두 등식의 일종인거죠.
(등호를 이용해 나타내잖아요.)
그럼 항등식이 문제로 나오면 어떻게 나올까요?
예제) $3x^2+2x+1=ax^2+bx+c$ 가 항등식일 때 상수 $a,b,c$ 는? |
이런 식으로 문제가 나올 수가 있습니다.
미리 항등식임을 알려주고 x를 구하는게 아니라 미정계수 $a,b,c$를 구하게 하는거죠.
그래서 이 문제에서는 조건이 3개가 나옵니다.
$3=a,2=b,1=c$
항등식 다양한 말로 변형도 가능해요.
아래 기술한 표현은 모두 항등식임을 나타내는 말입니다.
$3x^2+2x+1=ax^2+bx+c$가 항등식일 때~~~ $3x^2+2x+1=ax^2+bx+c$가 x 와 상관없이 성립할 때~~~ $3x^2+2x+1=ax^2+bx+c$ 가 모든 실수 x에 대하여 성립할 때~~~ |
이런 다양한 표현도 알아두세요.
항등식을 푸는 방법은 계수비교법과 수치대입법이 있어요.
계수비교법은 위의 문제처럼 각 항의 계수가 같다는 조건으로 푸는 방법이고 수치대입법은 특정한 수를 넣어서 푸는 방법이죠.
가령
$4x^2-3x+3=a(x+1)(x-1)+bx(x+1)+cx(x-1)$이 항등식일 때 상수 $a,b,c$ 를 구하라. |
라는 문제가 나왔다면 이건 우측 식을 전개해서 계수를 비교하는 것보다 x에 0과 1과 -1을 넣어서 나온 조건을 연립해서 푸는 게 더 효율적이겠죠?
왜냐면 항등식이니 x에 어떤 수를 넣어도 성립하기 때문이죠! 그 중 식정리가 편한 특정 몇 개 수를 넣어서 미지의 계수를 찾는 방법을 항등식의 수치대입법 이라고 얘기합니다.
그럼 항등식은 왜 나머지 정리 단원에서 나올까요?
그 이유를 알아봅시다.
식의 몫 표현법을 하기 전에 숫자의 몫 표현법을 알아볼게요.
우리 14를 3으로 나누어 봅시다.
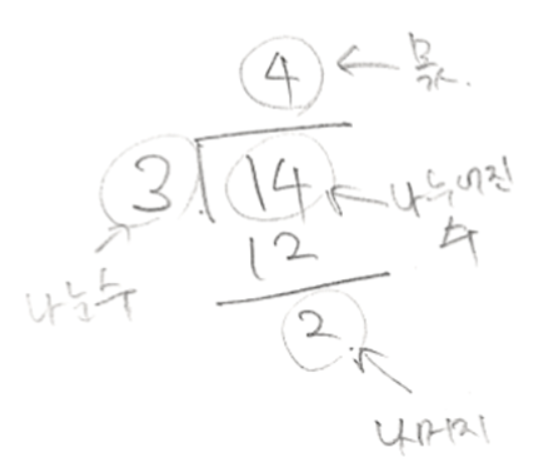
14를 3으로 나누면 몫이 4가 되고 나머지가 2가 됩니다.
그걸 식으로 나타내면 이렇게도 쓸 수 있겠죠?
나누어진수 = 나눈수*몫 + 나머지
$14=3\times4+2$
식도 마찬가지입니다.
나누어진 식 = 나눈식 * 몫 + 나머지 |
식의 나눗셈은 숫자의 나눗셈을 하듯이 최고차항을 없애주는 방식으로 진행합니다.
$x^3+2x^2+3x+4$를 $x-3$ 으로 나누어 볼게요.
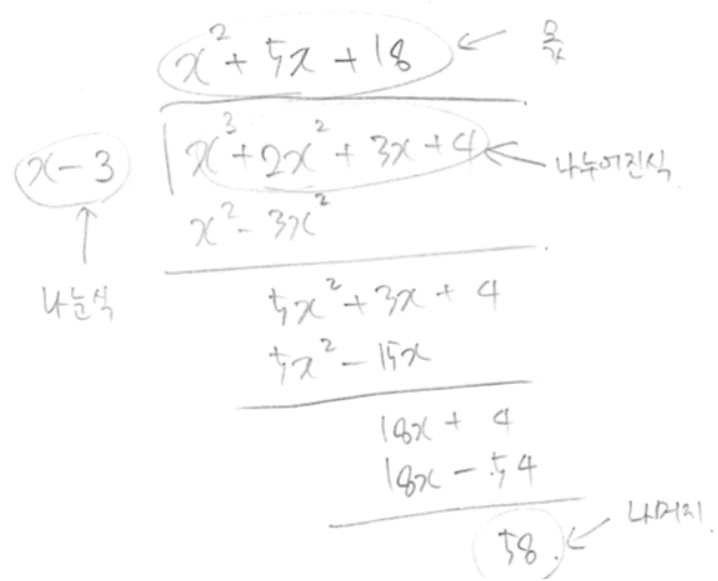
다항식의 나눗셈으로 몫이 $x^2+5x+18$임을 알았고 나머지가 58임을 알았습니다.
그럼 이 식을 이렇게 표현도 가능 하겠죠?
$x^3+2x^2+3x+4=(x-3)(x^2+5x+18)+58$
그럼 봅시다.
위 식은 방정식일까요 항등식일까요?
좌변 우변 같은 식
x에 무엇을 넣어도 성립하는 식
즉 항등식입니다.
만약에 몫은 필요 없고 나머지만 구하고 싶다면 어떻게 하면 좋을까요?
저 식에 3 을 넣는 겁니다.
그러면 굳이 다항식의 나눗셈을 복잡하게 할 필요가 없겠죠?
그래서 나머지를 쉽게 구하는 정리를 발견하게 됩니다.
나머지 정리 다항식 $f(x)$에서 $x-a$ 로 나눈 나머지를 $R$이라고 하면 $R=f(a)$ |
스토리가 길긴 하지만 나머지 정리는 정말 많은 단원에서 응용되는 개념입니다. 결과가 간단하고 응용되는 분야가 많기 때문이죠.
관심이 있으시다면 나머지 정리 연습문제도 한번 같이 풀어보세요.
#나머지정리 연습문제
http://samtoring.com/str/qstn_03/TST0001811
얘기가 길었네요.
스토리가 길지만 결론은 짧습니다. 그래서 여러분들이 꼼꼼히 알아두면 빠르게 쓸 수 있는 분야이기도 하지요.
나머지 정리를 사용할 때 나머지표현이 항등식이기 때문에 나머지정리단원에서 항등식을 같이 배운답니다.
그렇지만 항등식은 여러분들이 알게 모르게 자주자주 이용되고 있음을 기억하시기 바랍니다~!


