[수학이야기] 절댓값의 활용
절댓값만 보면 미쳐하는 학생들을 위해 살짝 정리해 봤습니다.
절댓값을 원점으로부터의 거리로 양수든 음수든 거리가 되는 순간 부호가 없어지는 수입니다.
만약 그 수가 양수라면 그냥 나오고 음수는 -를 곱해줘야 합니다.
그 말을 수식으로 쓰면
| $|x| = \begin{cases} (x \ge 0) \quad x, \\ (x \lt 0) \quad -x \end{cases}$ |
그런데 이걸 잘 모르는 친구는 많이 없어요.
어려워 하는 부분은 바로 활용에서 쓰일때죠.
그래서 절댓값 수식이 어떤 곳에서 많이 쓰이는지 봅시다.
( 범위가 넘어간다면 그러려니 하고 나중에 공부하세요~)
(1) $|x| \lt a$ 꼴 (수1 부등식)
$|x| \lt a \Leftrightarrow -a \lt x \lt a $
$|x| \gt a \Leftrightarrow x \lt -a , a \lt x $
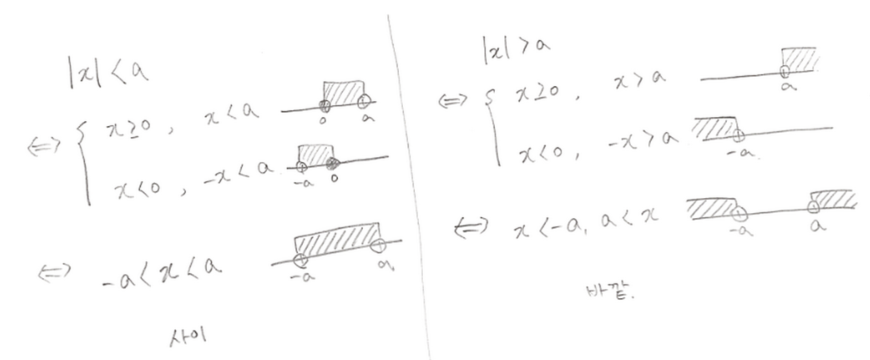
이 부등식은 보자마자 해석이 되어야 해요.
한번쯤은 원리에 입각해 증명해보고
나중에는 그 결과과정을 "사이" "바깥" 이라고 되네이면서
금방금방 그려야 합니다~!
(2) 절댓값으로 만들어진 불연속 함수. ( 미분과 적분 1 )
$f(x) = \frac{|x|}{x} $ 함수 구하기
이 함수는 절댓값 안에 있는 x의 범위를 양수일때 음수일때로 나누면
$\begin{cases} (x \gt 0 ) \frac{x}{x} = 1\\ (x \lt 0 ) \frac{-x}{x} = -1\\ (x = 0 ) 정의 안됨 \end{cases}$
저렇게 분자 분모에 같은 값을 곱해주고 나눠주면 약분이 될때 1또는 -1이 나와서 불연속 함수를 만들 수 있죠.
이 컨셉으로도 문제가 가끔 출제 됩니다.
(3) 다이아 몬드 도형 (단원 외)
$|x|+|y|=1$ 이런식으로 나오는 도형이 다이아몬드 형태의 함수가 그려진다는거!
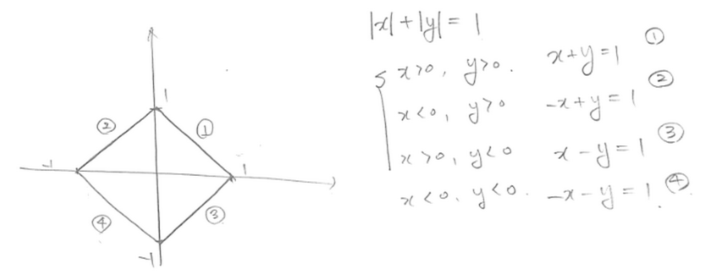
이건 |x| |y| 를 구간 나눠서 하나씩 그리면 직선이 연결되며 다이아 몬드 같은 모양을 그리게 되요.
그런데 이것의 확장버젼이 가끔 나오는데 그럴때는 x=0일때와 y=0 일때 생각해서 점을찍고
그 점을 이으시면 됩니다.
예를들어서
$3|x|+2|y|=6$인 그래프를 봅시다.
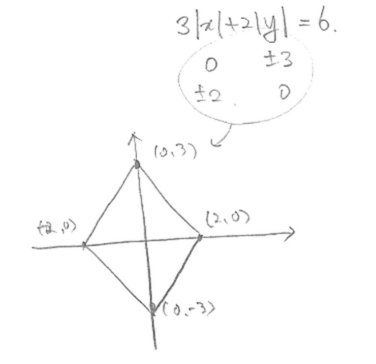
이런 모양의 함수가 있다면 x=0일때의 y값 +3, -3 을 찍고
y=0일때 x값 +2 ,-2 를 찍은 후 연결하면 함수를 쉽게 그릴 수 있어요.
(4) 함수의 그래프 (미분과 적분1)
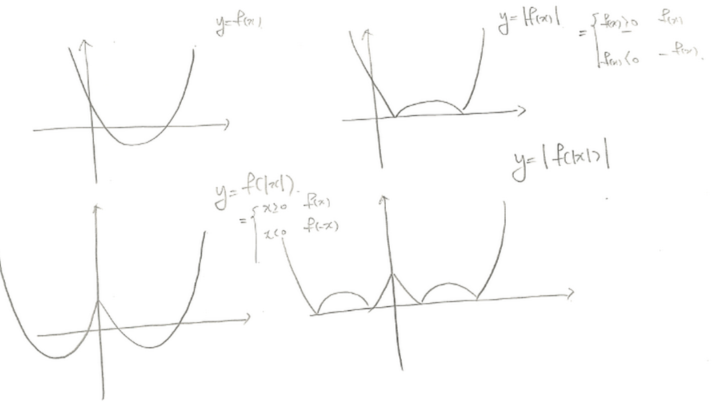
$y=|f(x)|$ , $y=f(|x|)$ 의 그래프
이 부분의 함수도 아주 자주 출제되는 유형입니다.
정의에 맞게 함수를 확장하면 아래와 같이 나오는데
아예이 꼴이 익숙해져서 금방 금방 그려질 수 있어야 해요.
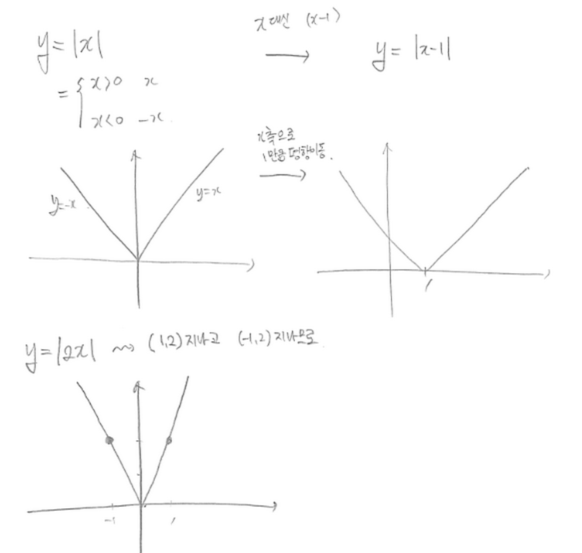
(5) 함수의 그래프 V자 꼴 함수 ( $y=|x|$의 그래프 )
$y=|x|$의 그래프도 아주 자주 출제되는 영역이죠.
기본꼴을 알아두시고 평행이동을 하거나 점을 찍어서 함수를 그리는게 편합니다.
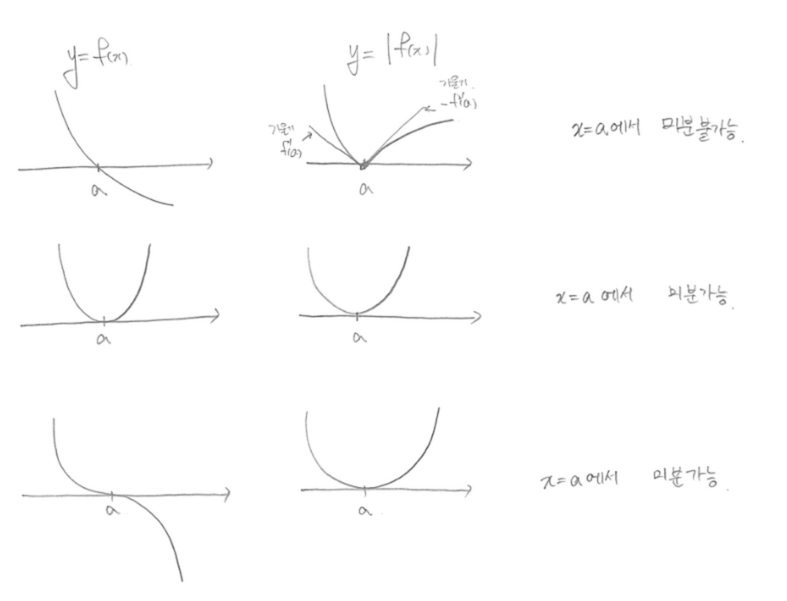
(6) 절댓값 함수와 미분 불가능한 점으로의 활용 ( 미분과 적분1 )
| 연속 함수 f(x)에서 $f(a)=0$ 이고 $f'(a) !=0$ 이면, $y=|f(x)|$는 $x=a$ 에서 미분 불가능 하다. |
(7) 그 이외의 꼴 ( 오히려 더 어렵고 복잡한 문제 )
그냥 최초 원리대로 그 안의 값이 음수일때와 양수일때 구간을 나누어서 풀어야 합니다.
귀찮지만 구간을 나누면 그제서야 푸는 방법이 보일거에요.
절댓값 포비아를 가진 학생들을 위해 정리해 봤구요
이해가 안되면 댓글 남겨주세요~!
더 필요한 문제가 있다면 샘토링에서 "절댓값의 활용" 이라고 검색을 해보세요~!

