정적분의 기하적 성질 산술적인 증명 (오류 찾으면 댓글 남기세요!! 꼭)
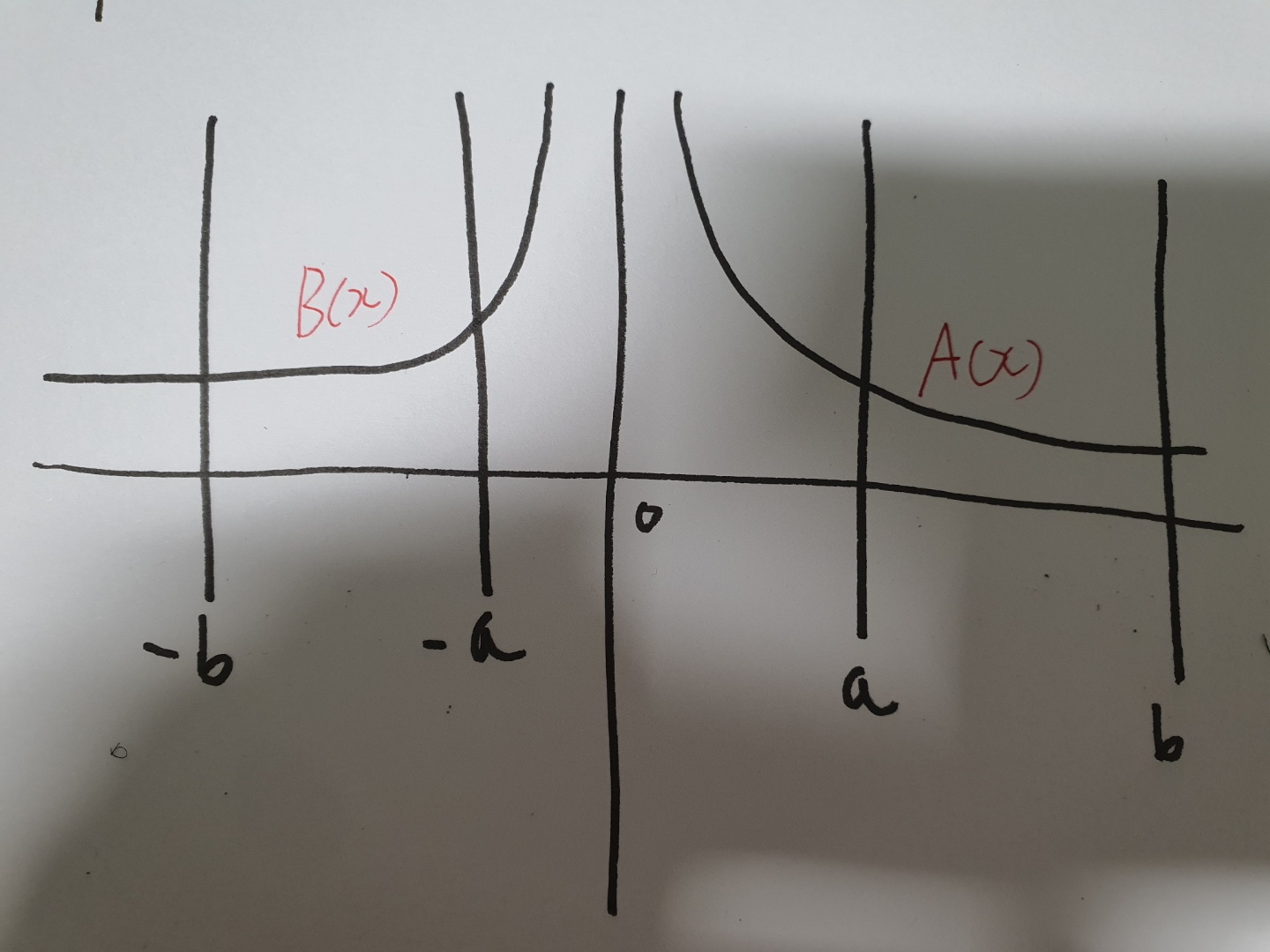
그림에서 볼수있듯히 서로 y축에대해 대칭관계의 두함수 A(x), B(x) 에서,
A(x) 를 b에서 a 까지 x 에 대해 적분한값 과,
B(x) 를 -a 부터 -b 까지 x 에 대해 적분한 값이 같은건 기하적으로 너무 명백한사실이다.
이걸 간단히 식으로 나타내면,
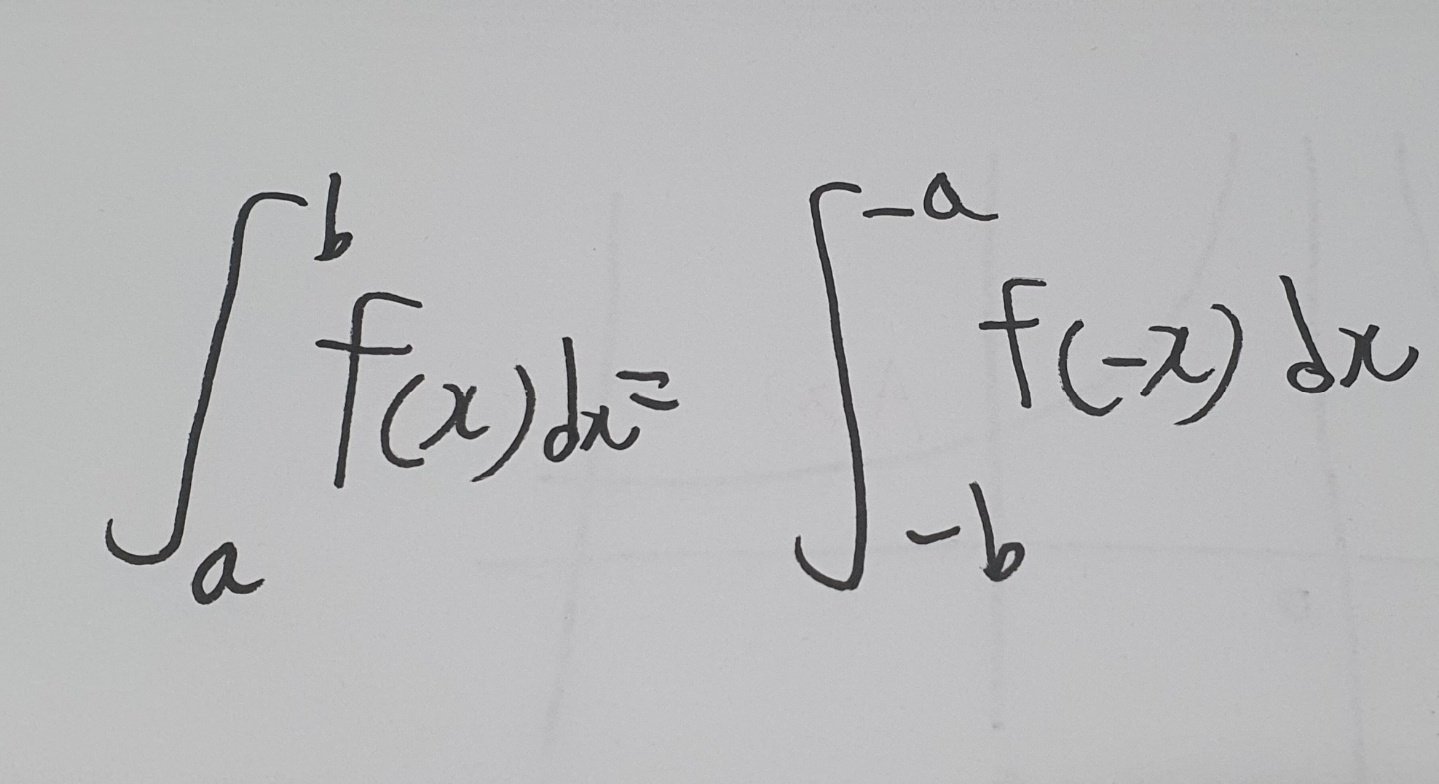
이렇게 된다.
이러한 성질을 다항함수 범위내에서 대수적으로 증명해보자.
최고차항이 최대 2n+1 인 다항함수 f(x) 를 식으로표현하면,
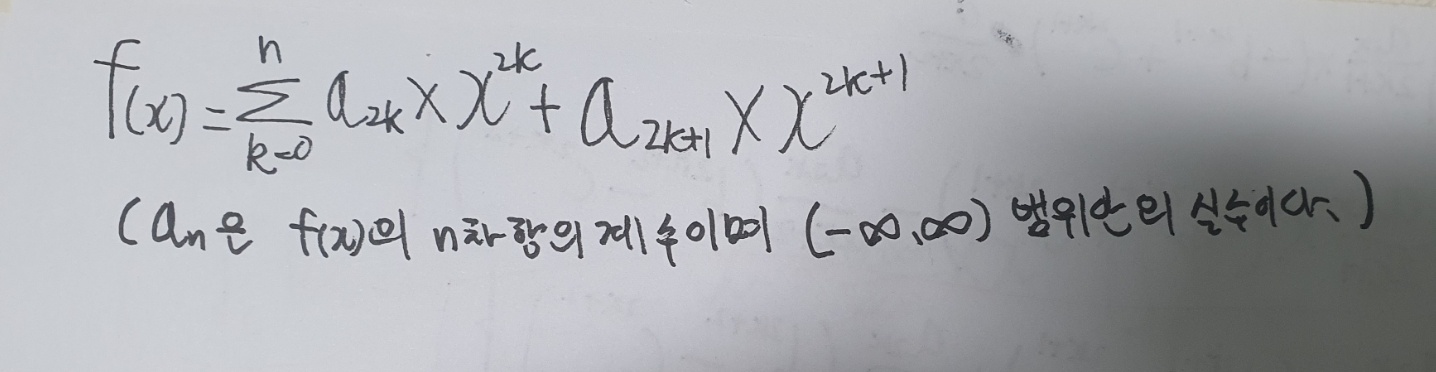이렇게된다.그리고 f(x) 에 -x 를 대입하면 x의 계수가 짝수이 첫번째항에는 영향을 주지못하고, 홀수인 두번째항의 부호를 바꾸므로
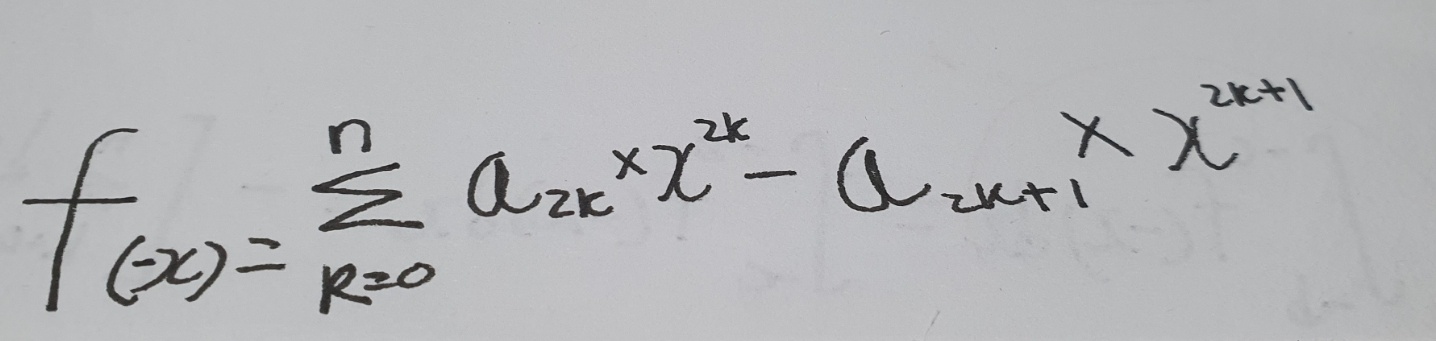
이렇게된다
이렇게 만들어진 f(x) 와 f(-x) 를 각각 b부터 c, -c부터 -b 까지 정적분을해보면,
(a 와 b 를 사용해 정적분을 나타내는것이 자연스럽겠지만 이미 a 가있어서 c를 사용하겠다)
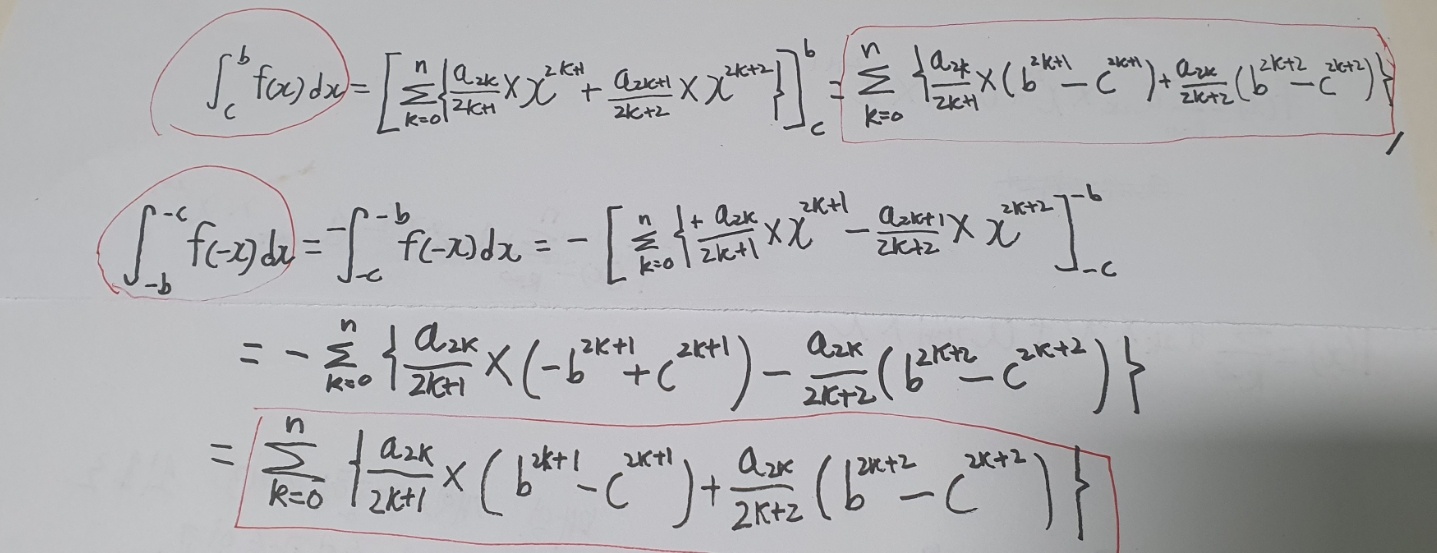
두 정적분에 값이 같게 나오므로(적분상수는 편의상 생략했다)
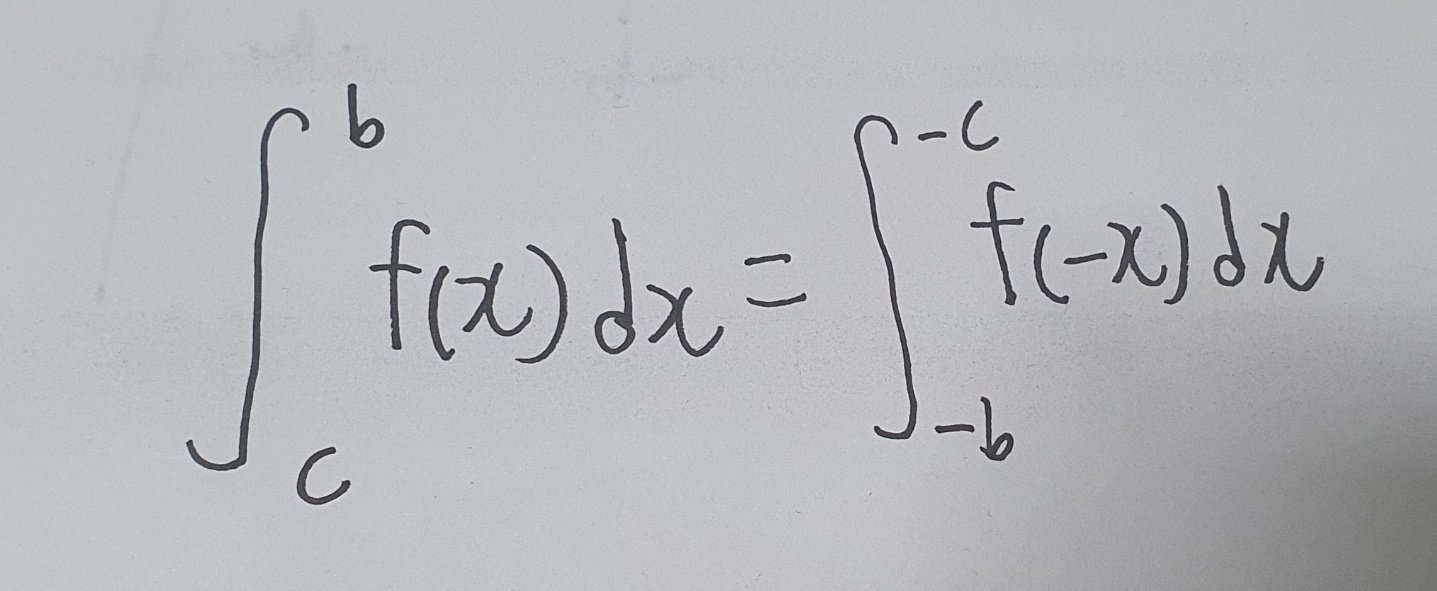
즉,
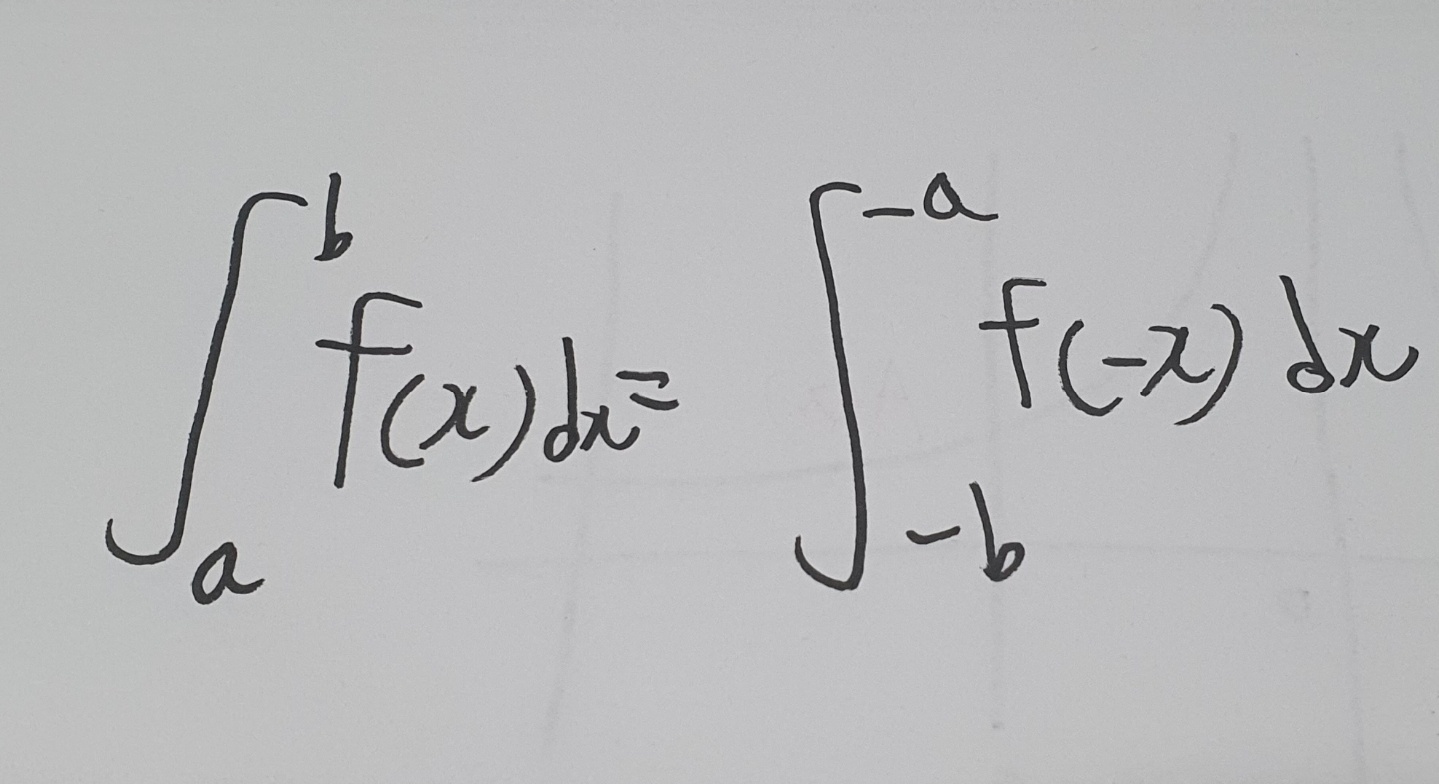
이식이 f(x) 가 다항함수라는 가정하에 성립함을 알수있다.
